6 Praxisorientierte Einführung in die Item-Response-Theorie mit dem Fokus auf das Rasch-Modell
Autorinnen: Tina Grottke, Philipp Möhrke, Marvin Rost
6.1 Motivation und konzeptuelle Herleitung
Bei vielen Tests geht es um die Frage, ob eine Testperson eine bestimmte Fähigkeit besitzt und damit eine Aufgabe richtig lösen kann. (Um Verwirrung zu vermeiden sei an dieser Stelle darauf hingewiesen, dass der Einfachheit halber nicht zwischen Aufgabe und Item unterschieden und genrell das Wort Aufgabe verwendet wird.) Diese Fähigkeit, die man messen möchte, ist aber meist nicht direkt zugänglich. Man spricht auch von einer latenten Fähigkeit. Der Zugang zu dieser Fähigkeit kann also nur über Aufgaben oder Fragen erfolgen, die die Testperson beantwortet und in deren Beantwortung sich die latente Fähigkeit zeigt.
Die Wahrscheinlichkeit, dass eine Person eine Aufgabe richtig lösen kann, hängt sowohl von der Fähigkeit der Person als auch von der Schwierigkeit der Aufgabe ab. Eine Aufgabe, die sehr oft richtig gelöst wird, könnte z.B. sehr einfach sein. Die Probanden könnten aber auch alle eine sehr hohe Fähigkeit haben, die ihnen erlaubt, die Aufgabe erfolgreich zu bearbeiten. Beide Punkte sind also auf den ersten Blick nicht voneinander zu trennen. Die Rasch-Modellierung (benannt nach dem dänischen Statistiker Georg Rasch (1901–1980)) löst dieses Problem. Das Rasch-Modell beschreibt wie wahrscheinlich es ist, dass ein Proband \(n\) ein Item \(i\) richtig löst in Abhängigkeit
- eines individuellen Personen- oder Personenfähigkeitsparameters \(\theta_n\) für jede Person, welche das Fähigkeitsausmaß der Person \(n\) beschreibt und
- eines Aufgaben- oder Aufgabenschwierigkeitsparameters \(\delta_i\), der den Schwierigkeitsgrad der Aufgabe \(i\) beschreibt.
Man erhält also aus einem Datensatz von richtigen oder falschen Antworten (ordinale Daten) der Personen zu verschiedenen Aufgaben ein kontinuierliches intervallskaliertes Maß in Form der Personenfähigkeitsparameter \(\theta_n\) und der Aufgabenschwierigkeitsparameter \(\delta_i\). Prinzipiell ist dieses Modell nicht auf dichotom zu bewertende Aufgaben beschränkt. Auch likert-skalierte Items sind z.B. möglich, sollen aber nicht Gegenstand dieses Beitrages sein.
Die Modellannahmen lauten wie folgt:
Das Maß der Fähigkeit jedes Probanden ist ausschließlich durch den Personenfähigkeitsparameter charakterisiert. Das heißt, dass es keine anderen Einflussfaktoren auf Seiten der Person gibt und ein sog. eindimensionales Modell berechnet wird.
Die Schwierigkeit der einzelnen Aufgaben ist ausschließlich durch den Aufgabenschwierigkeitsparameter charakterisiert. Die Schwierigkeit stellt also ebenfalls ein eindimensionales Merkmal dar.
Beide Parameter werden auf derselben Skala gemessen.
Die Leistungen einer Person hängt über alle Aufgaben hinweg – abgesehen von Zufall –, einzig von der Fähigkeit des Probanden und der Schwierigkeit der Aufgabe ab, nicht aber davon, welche anderen Aufgaben er oder sie bereits gelöst hat oder noch lösen wird.
Wie modelliert das Rasch-Modell nun aber genau das Antwortverhalten?
Der Zusammenhang zwischen der Lösungswahrscheinlichkeit einer Aufgabe, deren Schwierigkeit und der Fähigkeit der Person sollte jeden Fall derart sein, dass die Wahrscheinlichkeit einer richtigen Antwort mit wachsender Fähigkeit steigt. Im Idealfall könnte man annehmen, dass die Wahrscheinlichkeit einer richtigen Antwort für Personen mit einer niedrigen Fähigkeit bei null liegt und ab einer bestimmten Fähigkeit sprunghaft auf eins ansteigt. Ganz so ideal wird es aber nicht sein und der Übergangsbereich wird etwas weicher verlaufen. Explizit wird angenommen, dass sich die Wahrscheinlichkeit einer richtigen Antwort einer logistischen Funktion folgend entwickelt. Man setzt für die Wahrscheinlichkeit einer richtigen Antwort (mit 1 codiert) unter der Bedingung einer Personenfähigkeit \(\theta_n\) und Schwierigkeit der Aufgabe \(\delta_i\) an:
\[P(1|\theta_n, \delta_i) = \frac{\exp(\theta_n - \delta_i)}{1+\exp(\theta_n - \delta_i)} \]
Für eine Aufgabe mit dem Schwierigkeitsparameter 0 erhält man so folgenden Verlauf der Lösungswahrscheinlichkeit über den Fähigkeitsparameter.
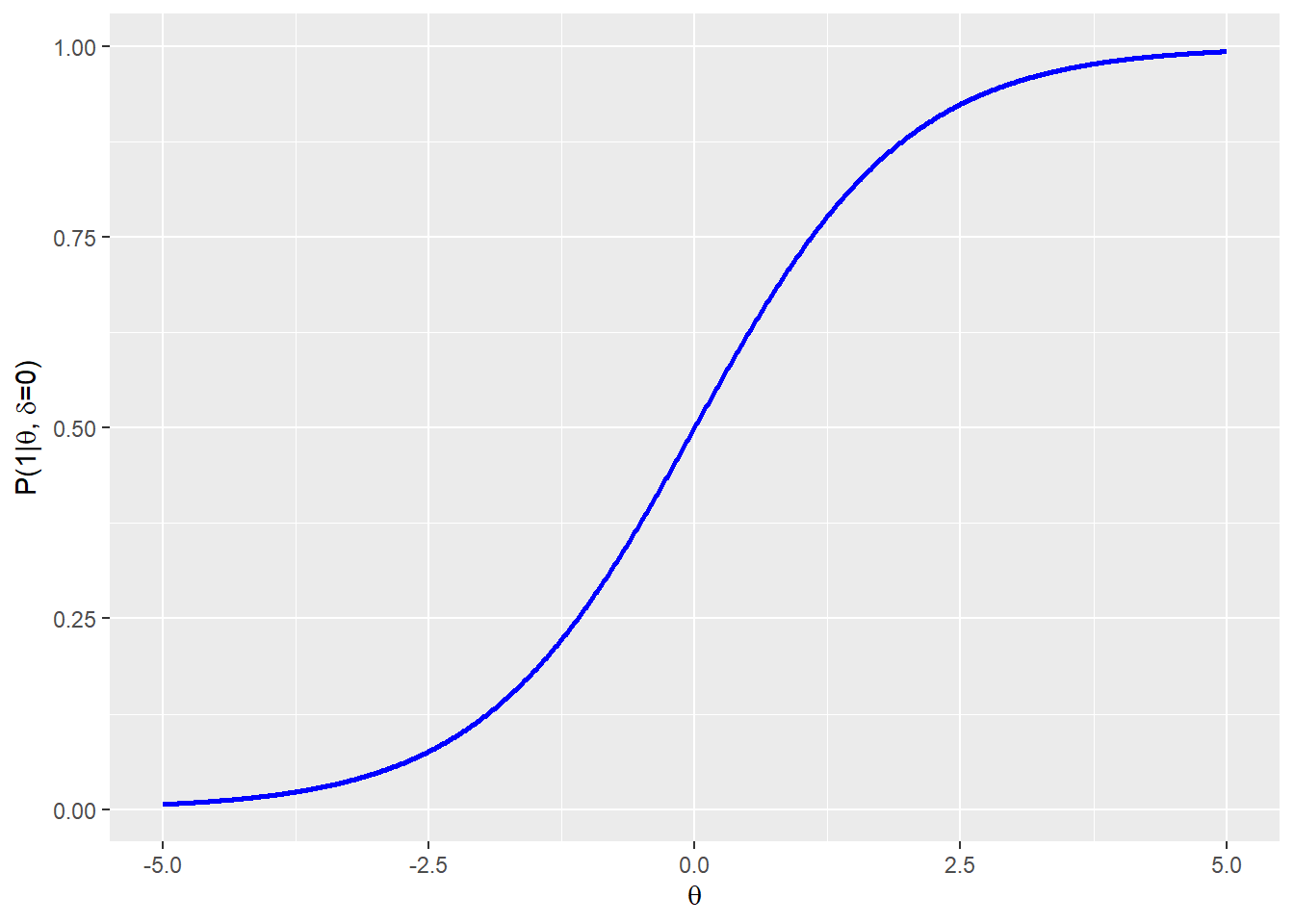 Personen mit einem Fähigkeitsparameter von -5.0 lösen diese Aufgabe also mit einer Wahrscheinlichkeit von etwa 0 (also wahrscheinlich nie), während Personen mit einem Fähigkeitsparameter von +5.0 die Aufgabe mit einer Wahrscheinlichkeit von etwa 1 (also wohl immer) lösen. Personen, deren Fähigkeitsparameter gerade so groß ist wie der Parameter der Aufgabenschwierigkeit, lösen die Aufgabe mit einer Wahrscheinlichkeit von 0.5 (also in etwa 50% der Fälle).
Personen mit einem Fähigkeitsparameter von -5.0 lösen diese Aufgabe also mit einer Wahrscheinlichkeit von etwa 0 (also wahrscheinlich nie), während Personen mit einem Fähigkeitsparameter von +5.0 die Aufgabe mit einer Wahrscheinlichkeit von etwa 1 (also wohl immer) lösen. Personen, deren Fähigkeitsparameter gerade so groß ist wie der Parameter der Aufgabenschwierigkeit, lösen die Aufgabe mit einer Wahrscheinlichkeit von 0.5 (also in etwa 50% der Fälle).
Im folgenden Plot ist die Lösungswahrscheinlichkeit einer Aufgabe in Abhängigkeit der Personenfähigkeit aufgetragen. Die Schwierigkeit der Aufgabe kann über den Schieberegler verändert werden. So kann z.B. verfolgt werden, wie sich die Lösungswahrscheinlichkeit einer Person mit Fähigkeitsparameter 0 ändert, wenn die Aufgabenschwierigkeit variiert wird.
Personen mit einem Personenfähigkeitsparameter von 0 würden also eine Aufgabe mit \(\delta = -0.5\) mit einer Wahrscheinlichkeit von 0.6 lösen, während sie eine Aufgabe mit \(\delta = 1.7\) nur mit einer Wahrscheinlichkeit von 0.15 lösen würde.
Schaut man sich die Formel für die Lösungswahrscheinlichkeit noch einmal an, sieht man, dass die Lösungswahrscheinlichkeit für Aufgabe \(i\) einzig von der Differenz der Parameter für Personenfähigkeit und Aufgabengabenschwierigkeit abhängt. Formt man die Gleichung etwas um, kann man auch schreiben \[\ln\left(\frac{P(1|\theta_n, \delta_i)}{1 - P(1|\theta_n, \delta_i)}\right) = \ln\left(\frac{P(1|\theta_n, \delta_i)}{ P(0|\theta_n, \delta_i)}\right) = \theta_n - \delta_i\]
Der natürliche Logarithmus der Chance (Wahrscheinlichkeit der richtigen Lösung geteilt durch Wahrscheinlichkeit der falschen Lösung) ist gleich der Differenz von Personenfähigkeits- und Aufgabenschwierigkeitsparameter. Plottet man die Chance gegen diese Differenz erhält man eine Gerade mit Steigung 1.
Diese Steigung und damit die Steigung des Übergangs von \(P\) wird für das Rasch-Modell also als fest angenommen. Die Steigung wird auch als Trennschärfe bezeichnet, weil Sie eine Aussage darüber liefert, wie klar ein Item zwischen den Fähigkeiten zweier Personen trennen kann.
Bei höheren Modellen wie dem 2-PL geht die Steigung als zusätzlicher Parameter ein.
6.1.1 Beispiel
Stellt man sich für ein Beispiel vor, dass die Kochkompetenz von Probanden gemessen werden soll. Dies stellt eine latente Fähigkeit dar, die nur über Testaufgaben auf diesem Gebiet erforscht werden kann. Ein entsprechender Test sollte aus verschieden schweren Aufgaben bestehen, wie etwa
- Zubereiten einer Tütensuppe (einfach)
- Kochen einer Tomatensoße nach Rezept (mittel)
- Kochen von Milchreis (mittel)
- Zubereitung eines mehrgängigen Menüs ohne Rezept für 4 Personen (schwer)
Welche Aufgabenschwierigkeitsparameter man diesen drei Aufgaben zuweisen würden, wie schwierig die Aufgaben also in Relation zueinander sind, ist nicht bekannt. Ob zum Beispiel Aufgabe 2 oder 3 schwieriger ist, ist schwer zu beurteilen. In realen Studien kann das bei der Erstellung der Aufgaben noch schwieriger sein.
Lässt man nun eine Zahl von Probanden alle vier Aufgaben in beliebiger Reihenfolge bearbeiten und vermerkt Erfolg (Ergebnis genießbar) oder Misserfolg (nicht genießbar), so erhält man eine Liste mit den Ergebnissen der Personen als Zeilen und den Aufgaben als Spalten. Diese Form wird auch als tidy Data (aufgeräumte/ordentliche Daten) bezeichnet und ist die bevorzugte Form, in der Daten vorliegen sollten (Wickham, 2014) oder * Tidy data.
Mit diesen Daten kann eine Rasch Analyse gemacht werden, mit welcher man ein intervallskaliertes Maß für sowohl die Kochfähigkeit jedes einzelnen Probanden erhält (die Personenfähigkeitsparameter \(\theta_n\)) als auch für die Schwierigkeit der einzelnen Aufgaben (die Aufgabenschwierigkeitsparameter \(\delta_i\)) erhält.
6.1.2 Wie wird der beste Fit gefunden?
Der beste Fit zwischen Modell und Daten, also der Satz von \(\theta_n\) und \(\delta_i\), der die beste Passung zwischen Modell und Daten liefert, kann über verschiedene Verfahren wie unter anderem das Least-quares- oder aber das Maximum-Likelihood-Verfahren gefunden werden (Linacre, 1999).
Bei letzterem wird durch ein iteratives Vorgehen, die sog. Likelihood-Funktion \[ L_n= \prod\limits_{i}P(1/0|\theta_n, \delta_i)\] für jede Personen \(n\) berechnet. Diese wird genau für den Personenfähigkeitsparameter maximal, für den die Wahrscheinlichkeit maximal wird, genau dieses Antwortverhalten auf die einzelnen Items zu erhalten. Es werden also die \(\theta_n\) gesucht, für die die \(L_n\) maximal werden.
Die Berechnung startet mit einer Schätzung der Itemschwierigkeit über den Anteil der Personen, die eine Aufgabe richtig bearbeitet haben \[ \delta_i = \log\left(\frac{p}{1-p}\right) \] und sucht den Satz von Personenfähigkeitsparametern \(\theta_n\), für den die Likelihood-Funktion maximal wird. Im nächsten Schritt wird mit diesen Satz von Personenfähigkeitsparametern \(\theta_n\), die Likelihood-Funktion bezüglich der Itemschwierigkeitsparameter \(\delta_i\) maximiert. So wird die Likelihood-Funktion immer weiter abwechseln bezüglich der \(\theta_n\) und der \(\delta_i\) maximiert. Dieser Vorgang sollte nach einer Zahl von Schritten konvergieren - sprich die Änderung der \(\theta_n\) und \(\delta_i\) wird immer kleiner und unterschreitet irgendwann einen festgelegten Wert. Dann wird der Prozess abgebrochen.
Für einen Test mit zwei Items mit den Schwierigkeitsparametern (\(\delta_1 = -1\), \(\delta_1 = 0.5\)) wäre die Likelihood-Funktion eines Probanden mit einer richtigen Antwort im ersten Item und einer falschen im zweiten Item:
\[L(\theta) = P(1|\theta, \delta_1 = -1) \cdot P(0|\theta, \delta_2 = 0.5)\\ = \left(\frac{\exp(\theta + 1)}{1+\exp(\theta + 1)}\right)\cdot\left(1-\frac{\exp(\theta - 0.5)}{1+\exp(\theta - 0.5)}\right)\]
Für diese muss nun das Maximum bezüglich \(\theta\) gefunden werden.
An dieser Stelle gibt es verschiedene Schätzmethoden für die Itemschwierigkeits- und Personenfähigkeitsparameter wie die Joint-Maximum-Likelihood-Schätzung (JML) und die Weighted Likelihood Schätzung (WLE), welche ein Bias in der Schätzung mit JML verringert. Die genauen Details dieser verschiedenen Verfahren sollen an dieser Stelle aber nicht weiter behandelt werden.
6.2 Der Datensatz
Der für diese Erklärung verwendete Datensatz stammt aus dem Paket TAM und hat das Format einer einfachen Matrix. Es handelt sich um simulierte Daten von 2000 Personen (als Zeilen) zu jeweils 40 Items (als Spalten). Die Spalten für die einzelnen Items sind mit I1 bis I40 bezeichnet. Eine Spalte für eine Personen-ID oder ähnliches gibt es nicht. Auch hat der Datensatz keine fehlenden Daten, d.h. zu jedem Probanden gibt es Daten zu jedem Item. Die Items selbst sind alle dichotom (richtig/falsch) und mit 1 und 0 codiert.
data(data.sim.rasch)
head(data.sim.rasch)## I1 I2 I3 I4 I5 I6 I7 I8 I9 I10 I11 I12 I13 I14 I15 I16 I17 I18 I19 I20 I21
## [1,] 1 1 1 1 1 1 0 1 0 1 1 0 0 1 1 1 1 1 1 1 0
## [2,] 0 1 0 0 0 1 1 1 0 1 1 1 1 1 0 0 1 0 1 0 0
## [3,] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1
## [4,] 1 0 1 1 0 1 1 1 0 0 1 1 1 0 0 1 1 0 0 0 0
## [5,] 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 0 0 1 1 1 1
## [6,] 1 1 1 0 0 1 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0
## I22 I23 I24 I25 I26 I27 I28 I29 I30 I31 I32 I33 I34 I35 I36 I37 I38 I39
## [1,] 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
## [2,] 0 0 1 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0
## [3,] 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 0 1
## [4,] 0 1 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0
## [5,] 0 1 1 1 1 1 0 1 0 0 0 1 1 1 0 1 0 0
## [6,] 1 0 0 1 0 1 1 0 0 0 1 0 0 0 0 0 0 0
## I40
## [1,] 0
## [2,] 0
## [3,] 1
## [4,] 0
## [5,] 0
## [6,] 06.3 Laden der benötigten Pakete und des Datensatzes
Da jede Anwendung der Software R die Nutzung von Paketen vorsieht, sind diese hier aufgelistet. Der geladene Datensatz wird mit dem “TAM”-Paket mitgeliefert.
library(TAM) # TAM-Paket als zentrales Paket
library(WrightMap) # zur Erzeugung von Wright-Maps
data(data.sim.rasch) # Lerndatensatz mit 2000 Personen & 40 Items, integriert in das TAM-Paket6.3.1 Paketquellen
- “TAM” (Robitzsch, Kiefer & Wu, 2020)
- “WrightMap” (Torres Irribarra & Freund, 2016)
6.4 Modellschätzung
Der folgende Code initiiert die Schätzung eines Rasch-Modells für den vorliegenden Datensatz. Das Listen-Objekt mod1PL mit 57 Sublisten wird erzeugt. Außerdem wird ein umfänglicher Konsolen-Output sichtbar. Dieser wird im Folgenden erläutert, es wird sich auf die mit Punkten getrennten Teilabschnitte bezogen.
mod1PL <- TAM::tam.mml(resp=data.sim.rasch)## ....................................................
## Processing Data 2022-08-02 11:43:04
## * Response Data: 2000 Persons and 40 Items
## * Numerical integration with 21 nodes
## * Created Design Matrices ( 2022-08-02 11:43:04 )
## * Calculated Sufficient Statistics ( 2022-08-02 11:43:04 )
## ....................................................
## Iteration 1 2022-08-02 11:43:04
## E Step
## M Step Intercepts |----
## Deviance = 84803.9272
## Maximum item intercept parameter change: 0.33272
## Maximum item slope parameter change: 0
## Maximum regression parameter change: 0
## Maximum variance parameter change: 0.125876
## ....................................................
## Iteration 2 2022-08-02 11:43:04
## E Step
## M Step Intercepts |---
## Deviance = 84201.8406 | Absolute change: 602.0866 | Relative change: 0.00715052
## Maximum item intercept parameter change: 0.044568
## Maximum item slope parameter change: 0
## Maximum regression parameter change: 0
## Maximum variance parameter change: 0.167316
## ....................................................
## Iteration 3 2022-08-02 11:43:04
## E Step
## M Step Intercepts |--
## Deviance = 84162.1461 | Absolute change: 39.6945 | Relative change: 0.00047164
## Maximum item intercept parameter change: 0.017468
## Maximum item slope parameter change: 0
## Maximum regression parameter change: 0
## Maximum variance parameter change: 0.069771
## ....................................................
## Iteration 4 2022-08-02 11:43:04
## E Step
## M Step Intercepts |--
## Deviance = 84156.6153 | Absolute change: 5.5308 | Relative change: 6.572e-05
## Maximum item intercept parameter change: 0.006594
## Maximum item slope parameter change: 0
## Maximum regression parameter change: 0
## Maximum variance parameter change: 0.026369
## ....................................................
## Iteration 5 2022-08-02 11:43:04
## E Step
## M Step Intercepts |--
## Deviance = 84155.879 | Absolute change: 0.7363 | Relative change: 8.75e-06
## Maximum item intercept parameter change: 0.00247
## Maximum item slope parameter change: 0
## Maximum regression parameter change: 0
## Maximum variance parameter change: 0.00966
## ....................................................
## Iteration 6 2022-08-02 11:43:04
## E Step
## M Step Intercepts |--
## Deviance = 84155.7823 | Absolute change: 0.0966 | Relative change: 1.15e-06
## Maximum item intercept parameter change: 0.000952
## Maximum item slope parameter change: 0
## Maximum regression parameter change: 0
## Maximum variance parameter change: 0.0035
## ....................................................
## Iteration 7 2022-08-02 11:43:04
## E Step
## M Step Intercepts |--
## Deviance = 84155.7696 | Absolute change: 0.0128 | Relative change: 1.5e-07
## Maximum item intercept parameter change: 0.000396
## Maximum item slope parameter change: 0
## Maximum regression parameter change: 0
## Maximum variance parameter change: 0.001263
## ....................................................
## Iteration 8 2022-08-02 11:43:04
## E Step
## M Step Intercepts |--
## Deviance = 84155.7678 | Absolute change: 0.0018 | Relative change: 2e-08
## Maximum item intercept parameter change: 0.00019
## Maximum item slope parameter change: 0
## Maximum regression parameter change: 0
## Maximum variance parameter change: 0.000455
## ....................................................
## Iteration 9 2022-08-02 11:43:04
## E Step
## M Step Intercepts |--
## Deviance = 84155.7674 | Absolute change: 4e-04 | Relative change: 0
## Maximum item intercept parameter change: 0.000111
## Maximum item slope parameter change: 0
## Maximum regression parameter change: 0
## Maximum variance parameter change: 0.000164
## ....................................................
## Iteration 10 2022-08-02 11:43:04
## E Step
## M Step Intercepts |-
## Deviance = 84155.7672 | Absolute change: 2e-04 | Relative change: 0
## Maximum item intercept parameter change: 7.9e-05
## Maximum item slope parameter change: 0
## Maximum regression parameter change: 0
## Maximum variance parameter change: 5.9e-05
## ....................................................
## Item Parameters
## xsi.index xsi.label est
## 1 1 I1 -1.9590
## 2 2 I2 -1.8570
## 3 3 I3 -1.7444
## 4 4 I4 -1.6407
## 5 5 I5 -1.5448
## 6 6 I6 -1.5344
## 7 7 I7 -1.3466
## 8 8 I8 -1.3499
## 9 9 I9 -1.2603
## 10 10 I10 -1.0469
## 11 11 I11 -1.0233
## 12 12 I12 -0.8563
## 13 13 I13 -0.8002
## 14 14 I14 -0.7447
## 15 15 I15 -0.5202
## 16 16 I16 -0.3962
## 17 17 I17 -0.3727
## 18 18 I18 -0.2298
## 19 19 I19 -0.1062
## 20 20 I20 -0.0522
## 21 21 I21 0.0376
## 22 22 I22 0.1044
## 23 23 I23 0.3343
## 24 24 I24 0.4232
## 25 25 I25 0.5209
## 26 26 I26 0.6415
## 27 27 I27 0.6443
## 28 28 I28 0.8484
## 29 29 I29 0.9395
## 30 30 I30 1.0179
## 31 31 I31 1.1160
## 32 32 I32 1.1372
## 33 33 I33 1.3117
## 34 34 I34 1.3149
## 35 35 I35 1.5559
## 36 36 I36 1.6198
## 37 37 I37 1.7039
## 38 38 I38 1.7490
## 39 39 I39 1.9352
## 40 40 I40 2.0502
## ...................................
## Regression Coefficients
## [,1]
## [1,] 0
##
## Variance:
## [,1]
## [1,] 1.404
##
##
## EAP Reliability:
## [1] 0.899
##
## -----------------------------
## Start: 2022-08-02 11:43:04
## End: 2022-08-02 11:43:04
## Time difference of 0.08912086 secs## Processing Data: Mit Uhrzeit und Datum versehener Diagnoseabschnitt.Calculated Sufficient Statisticsbestätigt für das Raschmodell, dass ausreichend viele Personen ausreichend viele Aufgaben bearbeitet haben. Weitere Details werden an dieser Stelle nicht ausgeführt, es sei lediglich darauf hingewiesen, dass die Berechnung bereits an dieser Stelle abgebrochen werden kann. Dies geschieht bspw. wenn ein fehlerhafter Datensatz vorliegt, der von der Funktion nicht lesbar ist.Iteration 1bisIteration 10: Hier werden iterativ die Modellparameter geschätzt (vgl. Abschnitt 4.1.2). Weil im Raschmodell nur die Schwierigkeit (item intercept parameter) und keine Steigung (item slope parameter) und kein Einfluss von Hintergrundvariablen (regression parameter) in das Modell eingebaut wurden, sind diese konstant \(0\). Gut erkennbar ist das kontinuierliche Absinken derDeviance-Änderung (Absolute change&Relative change): Die Berechnung konvergiert. DieDevianceselbst kann als Transformation der Likelihood (vgl. Abschnitt 3.1.2) verstanden werden. Sie ist also ein Maß für die Passung des Modells zu den Daten, die von Iteration zu Iteration besser wird, bis ein willkürlicher Grenzwert für die Änderung (Default beitam.mml(): \(0.0001\)) erreicht wurde.Item Parameters: Äquivalent zum Outputhead(mod1PL$item_irt), s. u. bei der Erklärung der Kennwerte aus dem Objektmod1PL$item.Regression Coefficients: Es wurden keine weiteren Hintergrundvariablen (z. B. Alter oder Gender) in das Modell eingefügt. Daher ist der Wert in diesem Fall \(0\).Variance: Varianz des berechneten Parameters.EAP Reliability: Expected-A-Posteriori-Reliabilität. Über ein statistisches Verfahren berechnetes Maß für die Reliabilität des Testinstruments. Kann in erster Näherung analog zu Cronbachs-\(\alpha\) aus der klassischen Testtheorie interpretiert werden. Wichtiger Hinweis: Die EAP-Reliabilität ist ein zuverlässiger Schätzer für Populationen, nicht jedoch für Einzelpersonen!
Folgend wird das Dataframe-Objekt mod1PL$item aus dem Listen-Objekt mod1PL ausgewählt und mit der Funktion head() die ersten 6 von insgesamt 40 Einträgen ausgegeben. Es enthält verschiedene Spalten mit deskriptiven Kennwerten:
head(mod1PL$item)
## item N M xsi.item AXsi_.Cat1 B.Cat1.Dim1
## I1 I1 2000 0.8270 -1.959017 -1.959017 1
## I2 I2 2000 0.8145 -1.857027 -1.857027 1
## I3 I3 2000 0.8000 -1.744435 -1.744435 1
## I4 I4 2000 0.7860 -1.640747 -1.640747 1
## I5 I5 2000 0.7725 -1.544800 -1.544800 1
## I6 I6 2000 0.7710 -1.534362 -1.534362 1item: Laufnummer der jeweiligen Items.N: Anzahl an Personen, die das jeweilige Item bearbeitet haben.M: Deskriptive Schwierigkeit des Items (\(M = \frac{N_{korrekt}}{N_{gelöst}}\)).xsi.item: xsi wird ausgesprochen wie geschrieben und bezieht sich auf den griechischen Buchstaben (\(\xi\)). Der \(\xi\)-Parameter ist die, mit dem Modell geschätzte, Aufgabenschwierigkeit auf der Skala von \(-\infty\) bis \(\infty\) mit 0 als Mittelwert. Übliche Werte in der Praxis liegen zwischen -3 bis 3. Eine Aufgabe mit Schwierigkeit \(\xi=1\) ist dabei schwerer als eine Aufgabe mit Schwierigkeit \(\xi=0\). Oft findet man den Schwierigkeitsparameter auch unter anderen griechischen Buchstaben in der Literatur, z. B. \(\delta\) oder \(\beta\). TAM übernimmt die Notation mit \(\beta\) unter der Bezeichnung IRT parametrization. Siehe dazu die ersten 6 von 40 Einträgen im folgenden Dataframe-Objektmod1PL$item_irt.
head(mod1PL$item_irt)
## item alpha beta
## 1 I1 1 -1.959017
## 2 I2 1 -1.857027
## 3 I3 1 -1.744435
## 4 I4 1 -1.640747
## 5 I5 1 -1.544800
## 6 I6 1 -1.534362AXsi_.Cat1: Da im gezeigten Beispiel nur ein eindimensionales Modell ohne weitere Bedingungen berechnet wurde, entspricht der Wert dem \(\xi\)-Parameter, d. h. der Schwierigkeit. Unter anderen Bedingungen (beispielsweise Mehrdimensionalität, oder verschiedenen Testheftpositionen der Aufgabe), können verschiedende, bedingte Schwierigkeiten auftreten. Dazu ein fiktives, vereinfachtes Beispiel: Eine Aufgabe ist in zwei verschiedenen Testheften zu finden. In Testheft Nr. 1 ist sie immer die erste Aufgabe, in Testheft Nr. 2 ist sie immer die letzte Aufgabe. Die Testheftposition kann im statistischen Modell berücksichtigt werden und es würden dann zwei testheftabhängige Schwierigkeitsparameter berechnet, die sich alsAXsi_.Cat1undAXsi_.Cat2im Output wiederfinden würden.B.Cat1.Dim1: Steigungsparameter. Im eindimensionalen 1PL-Modell wird der B-Parameter nicht berechnet, sondern auf \(B=1\) fixiert. Oft findet man den Steigungsparameter auch unter der Bezeichnung \(\alpha\) (siehe Output oben zuxsi.item).
Eine Zusammenfassung des Modellobjekts mit allen oben ausgeführten Kennwerten kann über den Befehl summary(mod1PL) erhalten werden.
6.4.1 Deutung der Aufgabenschwierigkeiten
Die erhaltenen Schwierigkeitsparameter stehen unter dem Vorbehalt, dass das Rasch-Modell gültig ist (Wu, Tam & Jen, 2016, S. 139ff.). Sie setzen die Aufgaben nun jenseits von subjektiven Einflüssen miteinander in Beziehung. War eine Schwierigkeitseinschätzung a-priori (bspw. durch ein Expertenrating) noch von zahlreichen, personenabhängigen Einflüssen getragen, sind nun die Bearbeitungserfolge durch die Zielgruppe in der quantitativ-empirischen Erhebung integriert: Die Schwierigkeiten wurden gemessen und nicht über den Daumen gepeilt. Noch vor weiterführenden Analysen können die so erhaltenen, quantitativen Befunde wiederum durch qualitative Urteile abgeglichen werden:
- Gibt es Aufgaben, die erwartungsgemäß schwerer/leichter waren als andere?
- Gibt es Aufgaben, deren Schwierigkeiten nicht erwartungskonform sind?
- War eine Aufgabe vielleicht zu einfach, weil die Distraktoren unpassend gewählt waren?
- …
Die Aufgabenentwicklung führt so in einem Zusammenspiel aus objektiven Kriterien und subjektiver Synthese (bspw. Erfahrung von PraktikerInnen, Literaturrecherche, curriculare Anforderungen) zu validen und reliablen Testinstrumenten.
6.5 Erzeugen einer Wright-Map
Mit einem Mathematiktest für GrundschülerInnen wird es kaum möglich sein, verschiedene Studierende der Mathematik und ihrer Fähigkeit zu rechnen zu unterscheiden. Analoges gilt für einen zu schweren Test für die GrundschülerInnen.
Für Leistungstests ist also eine breite Verteilung von Aufgabenschwierigkeiten über die Personenfähigkeiten wünschenswert. Wright-Maps erlauben eine Prüfung der Abdeckung, indem sie die Aufgabenschwierigkeiten und die Personenfähigkeiten grafisch miteinander in Beziehung setzen. Es wird dabei auf einen Blick deutlich, wenn in einem bestimmten Schwierigkeits-/Fähigkeitsintervall zu wenige oder zuviele Aufgaben vorliegen. Dies ist insbesondere in der Pilotierungsphase eines Tests hilfreich.
Das folgende Code-Beispiel schätzt die Personenfähigkeiten und schreibt sie über die Funktion tam.wle in das Objekt thetas_1pl. Außerdem werden die Aufgabenschwierigkeiten separat als Objekt item_xsis_1pl abgespeichert um anschließend mit der Funktion wrightMap() eine automatische Visualisierung zu erhalten (Abb. 6.1).
thetas_1pl <- tam.wle(mod1PL)
item_xsis_1pl <- mod1PL$xsi$xsi
wrightMap(thetas_1pl$theta, item_xsis_1pl,
main.title = "Beispiel für Wright-Map",
axis.persons = "Fähigkeitsverteilung",
axis.items = "Aufgaben")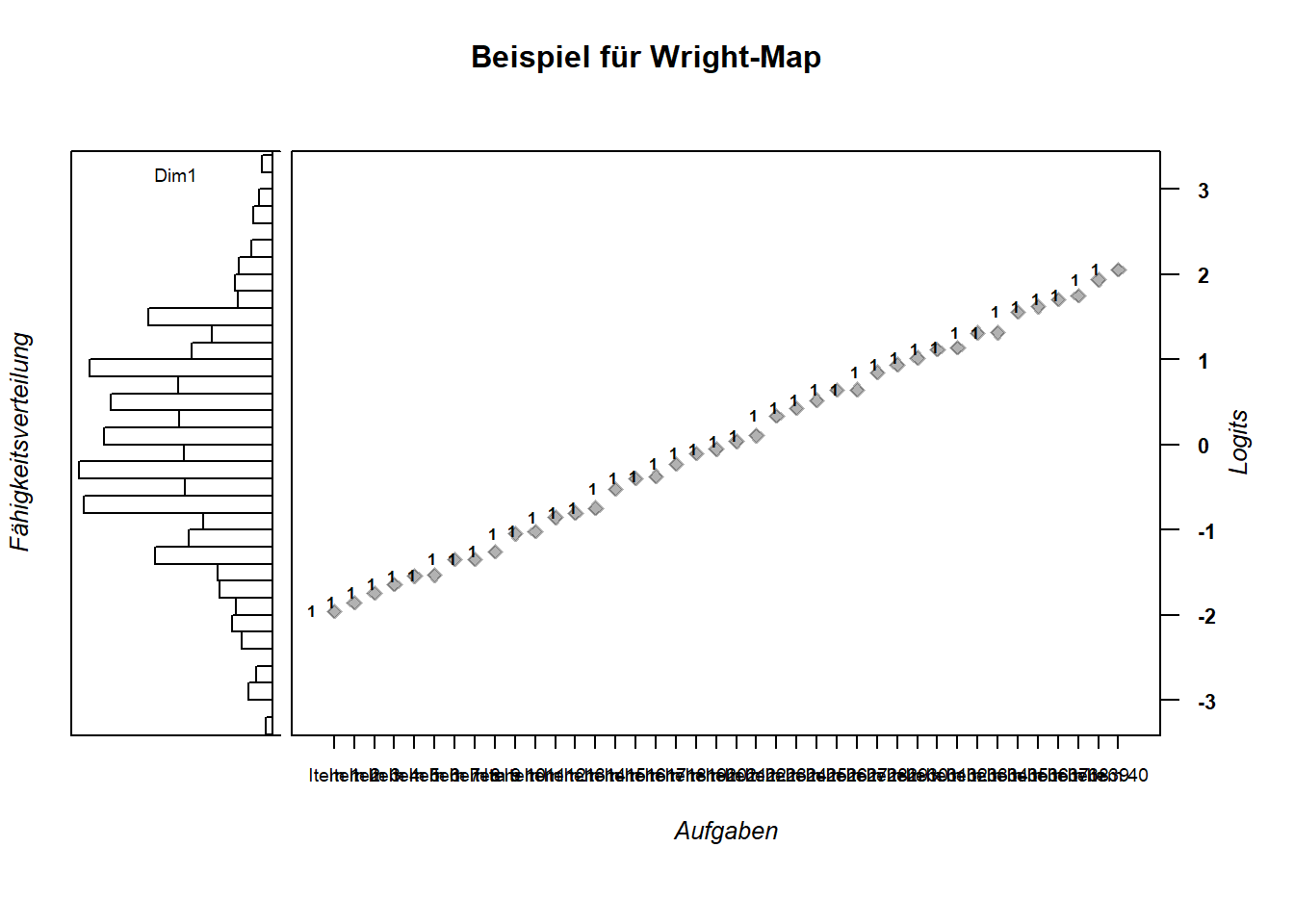
Figure 6.1: Eine Variante für eine Wright-Map.
Gut erkennbar ist die Fähigkeitsverteilung in Dimension 1 (schmaleres Panel links) und die numerische Zuordnung der Aufgaben zu dieser Dimension (breiteres Panel rechts). Ebenfalls deutlich wird die Äquivalenz von Personenfähigkeiten und Aufgabenschwierigkeiten, erkennbar an der Logit-Skala auf der rechten Seite.
Ungünstig ist die kategorische Aufgaben-Achse. Da der Datensatz 40 Aufgaben enthält, resultiert ein Overplot der Aufgaben-Namen, dem mit einer Alternativdarstellung begegnet werden kann (Abb. 6.2).
wrightMap(thetas_1pl$theta, item_xsis_1pl,
item.side = itemClassic,
main.title = "Beispiel für Wright-Map",
axis.persons = "Fähigkeitsverteilung",
axis.items = "Aufgabenverteilung")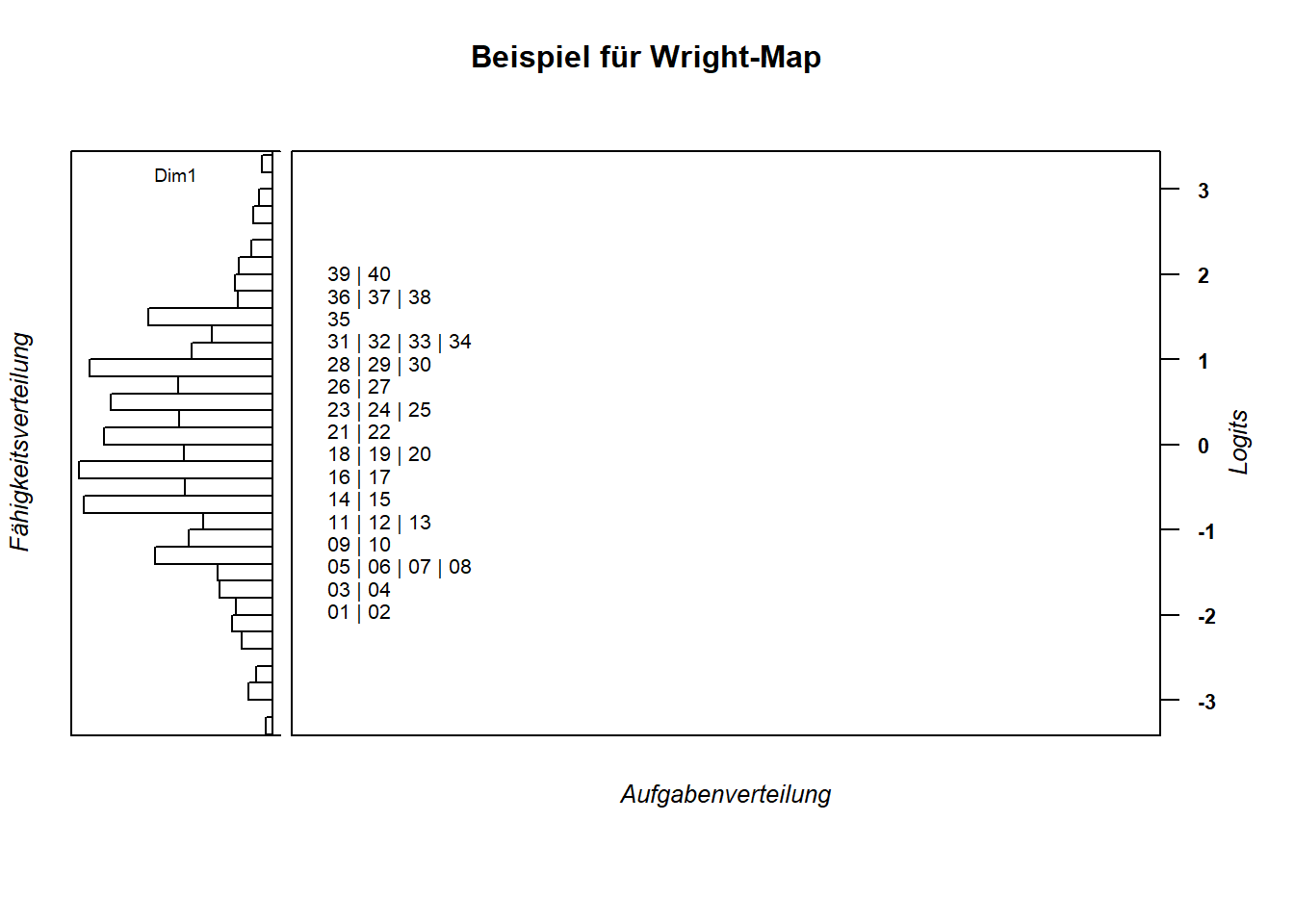
Figure 6.2: Eine Alternative Darstellung der Wright-Map.
In diesem Fall ist gut zu sehen, wie die Aufgaben - markiert durch ihren Laufindex aus dem Datensatz - von unten nach oben schwieriger werden. Außerdem erkennbar: Die Aufgaben sind näherungsweise uniform über das Schwierigkeits-/Fähigkeitsintervall verteilt. Außerdem stehen für sehr leistungsstarke und -schwache Personen (Ränder der Fähigkeitsverteilung) empirisch keine äquivalent schwierigen Aufgaben zur Verfügung.
6.5.1 Deutung der Wright-Maps
Wäre dieser Datensatz aus einer realen Studie entstanden, wäre die Nachkonstruktion von sehr schweren und sehr leichten Aufgaben zu empfehlen. Darüber hinaus halten sich im mittleren Fähigkeitsniveau die meisten Personen auf. Um zwischen diesen besser differenzieren zu können, wären auch dort mehr Aufgaben hilfreich.
6.6 ICC (Item Characteristic Curve)
6.6.1 Input
Item Characteristic Curves (kurz: ICC) geben die Lösungswahrscheinlichkeit als Funktion der Fähigkeit der Testpersonen an. Dabei stellt die y-Achse die Lösungswahrscheinlichkeit und x-Achse die Personenfähigkeit dar.
Um Verwirrungen zur Begrifflichkeit Item und Aufgabe zu vermeiden, wird an dieser Stelle darauf hingewiesen, dass Items hier im vereinfachten Sinne einer Aufgabe entsprechen.
6.6.2 R-Befehl für Generierung der ICC in TAM
Das Ausführen der folgenden Funktion führt zur Erstellung der ICC für Item 20 sowie der Anteile richtiger Lösungen von sechs Personenfähigkeitsgruppen zu dieser Aufgabe. Wie im folgenden erläutert, lässt sich damit untersuchen, inwiefern die Modellvorhersage (Rasch-Modell mit den auf Basis des Antwortverhaltens geschätzten Schwierigkeits- und Fähigkeitsparametern) und die Daten (tatsächliches Antwortverhalten) voneinander abweichen.
plot(mod1, items = 20, ngroups = 6, export = FALSE) # export = FALSE verhindert separates Abspeichern der .png-Datei## Iteration in WLE/MLE estimation 1 | Maximal change 0.8281
## Iteration in WLE/MLE estimation 2 | Maximal change 0.4335
## Iteration in WLE/MLE estimation 3 | Maximal change 0.0883
## Iteration in WLE/MLE estimation 4 | Maximal change 7e-04
## Iteration in WLE/MLE estimation 5 | Maximal change 0
## ----
## WLE Reliability= 0.894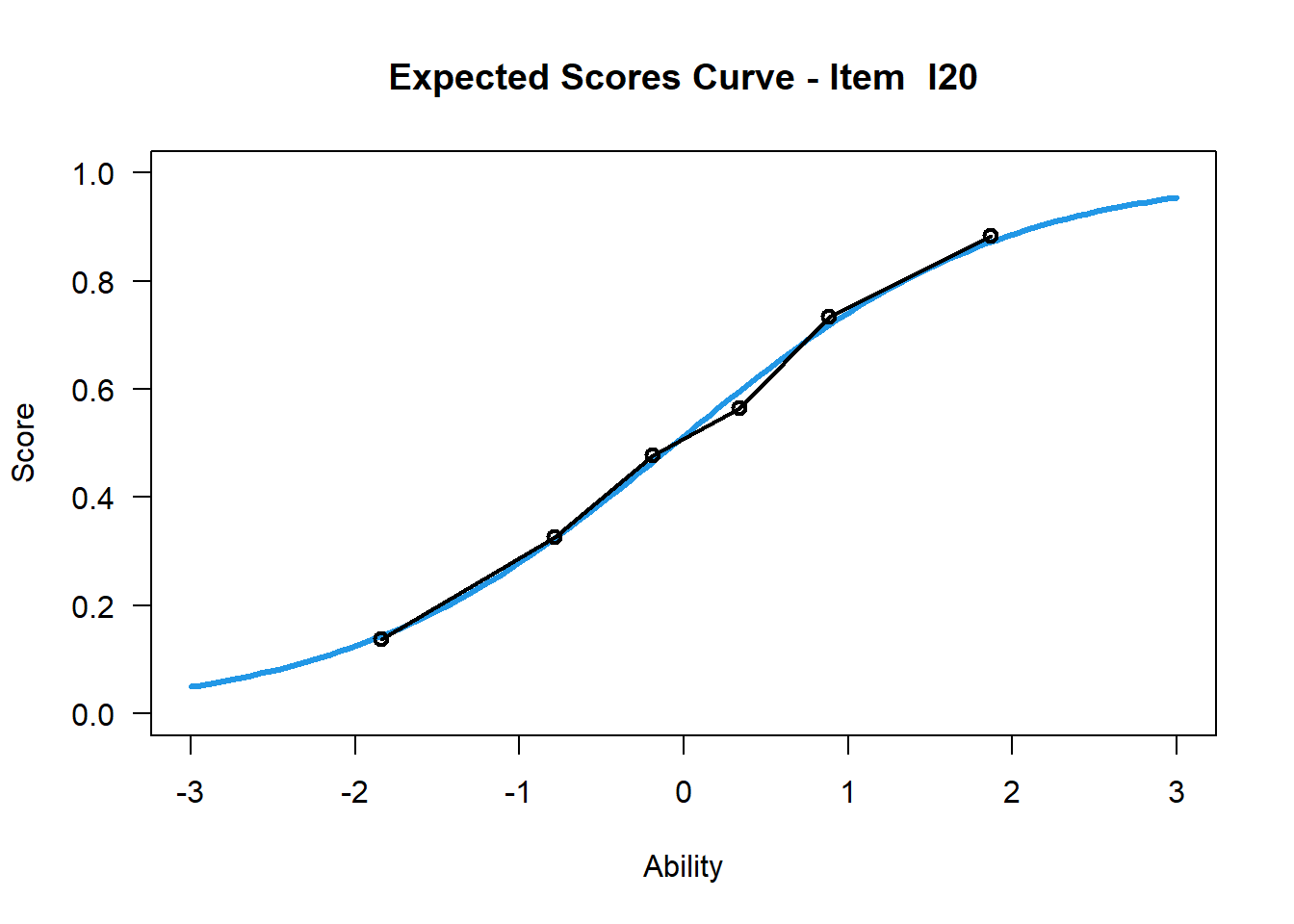
Eine ICC kann alleine unter Kenntnis des Schwierigkeitsparameters der Aufgabe erstellt werden. Sie lässt sich nutzen, um grafisch zu beurteilen, inwiefern das tatsächliche Lösungsverhalten der Testpersonen von dem Verhalten, welches mithilfe des Rasch-Modells vorhergesagt wird, abweicht.
Naiv würde man davon ausgehen, dass man nur die tatsächlichen Lösungswahrscheinlichkeiten in Abhängigkeit von den Fähigkeiten der Testpersonen eintragen müsste (so macht man es auch bspw. im Physikunterricht, bei der ersten grafischen linearen Regression). Diese Lösungswahrscheinlichkeiten sind aber nicht für einzelne Testpersonen, sondern nur für Gruppen, direkt beobachtbar. Aufgrunddessen werden die Testpersonen in Fähigkeitsgruppen eingeteilt (Binning). Der Prozentsatz einer bestimmten Gruppe, der die Aufgabe richtig gelöst hat, entspricht dann der Lösungswahrscheinlichkeit.
Die Angaben MLE (Maximum Likelihood Estimates) und WLE (Weighted Likelihood Estimates) in der Ausgabe stehen für das angewandte Verfahren zur Schätzung der Personenfähigkeiten. Bei den durch die MLE geschätzten Personenfähigkeiten kommt es jedoch zu Verzerrungen, sodass auf den WLE zurückgegriffen wird (Trendtel, Pham & Yanagida, 2016, S. 202).
6.6.3 Interpretation ICC im Rasch-Modell (Wu et al., 2016)
Ausführungen beziehen sich auf Item 20, s. obigen Plot
blaue Kurve: Modellkurve (vom Modell vorhergesagter Zusammenhang zw. Fähigkeit und Lösungswahrscheinlichkeit) –> Testpersonen mit einer Fähigkeitsausprägung von 1, lösen das Item mit 75%iger Wahrscheinlichkeit richtig
schwarze Kurve: empirische Kurve (beobachtete Lösungswahrscheinlichkeit bzw. Lösungsquote) –> etwa 76 % der Testpersonen mit der Fähigkeitsausprägung (ability) = 1 lösten das Item richtig
–> Bei diesem Beispiel (Item 20) liegt eine gute Passung beider Kurven vor, d.h. das Modell beschreibt das Lösungsverhalten bei diesem Item sehr gut.
6.6.3.1 Misfits
Für die Beurteilung von Items, kann die Passung der empirischen Kurve zur Modellkurve herangezogen werden. Dabei muss nicht immer die empirische Kurve gut zur Modellkurve passen –> Misfits
Es wird dabei zw. Overfit und Underfit unterschieden, wobei der wMNSQ-Wert (= standardized weighted mean square), welcher auch als Infit-Wert geführt wird, bei der Beurteilung eine Orientierung bieten kann “Die Infit-Statistik ist der mit den Varianzen […] gewichtete Mittelwert, sodass Personen mit einer Fähigkeit näher bei der Itemschwierigkeit des betrachteten Items ein höheres Gewicht bekommen als Personen, deren Fähigkeit weiter weg liegt.” (Trendtel et al., 2016, S. 209). Dabei sei darauf hingewiesen, dass trotz guter wMNSQ-Werte (Werte um 1), die Passung zwischen empirischer Kurve und Modellkurve als schlecht beurteilt werden kann. “Fit mean-square statistic is testing whether the slope of the observed ICC is the same as the theoretical ICC” (Wu et al., 2016, S. 145). Die Outfit-Statistik, zu der der unweighted mean square (MNSQ-Outfit) gehört, wird in Large-Scale-Assessments kaum Bedeutung zugetragen, sodass sich auf die Infit-Statistik fokussiert wird (Trendtel et al., 2016, S. 209).
Overfit: wMNSQ-Wert (Infit) < 1; empirische Kurve steiler als Modellkurve; entspricht hoher discrimination –> Item unterscheidet Testpersonen verschiedener Fähigkeitsausprägungen besser als andere Items im Test
Underfit: wMNSQ-Wert (Infit) > 1; empirische Kurve flacher als Modellkurve; entspricht geringerer discrimination
Es wird empfohlen, Items mit einem Overfit zu behalten und Items mit einem Underfit aus dem Test zu entfernen (Wu et al., 2016, S. 153).
6.6.4 Gegenüberstellung leichtes - schweres Item
mod1$xsi # Itemschwierigkeiten xsi aller Items## xsi se.xsi
## I1 -1.95901708 0.06465854
## I2 -1.85702665 0.06311470
## I3 -1.74443543 0.06153710
## I4 -1.64074652 0.06019663
## I5 -1.54480023 0.05904820
## I6 -1.53436162 0.05892844
## I7 -1.34662700 0.05694173
## I8 -1.34987110 0.05697344
## I9 -1.26034689 0.05613124
## I10 -1.04688427 0.05438831
## I11 -1.02329441 0.05421784
## I12 -0.85632426 0.05313222
## I13 -0.80020663 0.05281391
## I14 -0.74473359 0.05252176
## I15 -0.52021484 0.05156219
## I16 -0.39622299 0.05118169
## I17 -0.37267520 0.05112121
## I18 -0.22981140 0.05083401
## I19 -0.10615527 0.05069507
## I20 -0.05221976 0.05066614
## I21 0.03760166 0.05066059
## I22 0.10436417 0.05069098
## I23 0.33428538 0.05102212
## I24 0.42316815 0.05124518
## I25 0.52089569 0.05155264
## I26 0.64154518 0.05202355
## I27 0.64425227 0.05203529
## I28 0.84842093 0.05307253
## I29 0.93949280 0.05363422
## I30 1.01792547 0.05416852
## I31 1.11604992 0.05490459
## I32 1.13721663 0.05507343
## I33 1.31166540 0.05660515
## I34 1.31487135 0.05663570
## I35 1.55588652 0.05919171
## I36 1.61976438 0.05995850
## I37 1.70391234 0.06102867
## I38 1.74904684 0.06163154
## I39 1.93524957 0.06434122
## I40 2.05021754 0.06620206Item 1
plot(mod1, items = 1, ngroups = 6, export = FALSE) # xsi = -1.96## Iteration in WLE/MLE estimation 1 | Maximal change 0.8281
## Iteration in WLE/MLE estimation 2 | Maximal change 0.4335
## Iteration in WLE/MLE estimation 3 | Maximal change 0.0883
## Iteration in WLE/MLE estimation 4 | Maximal change 7e-04
## Iteration in WLE/MLE estimation 5 | Maximal change 0
## ----
## WLE Reliability= 0.894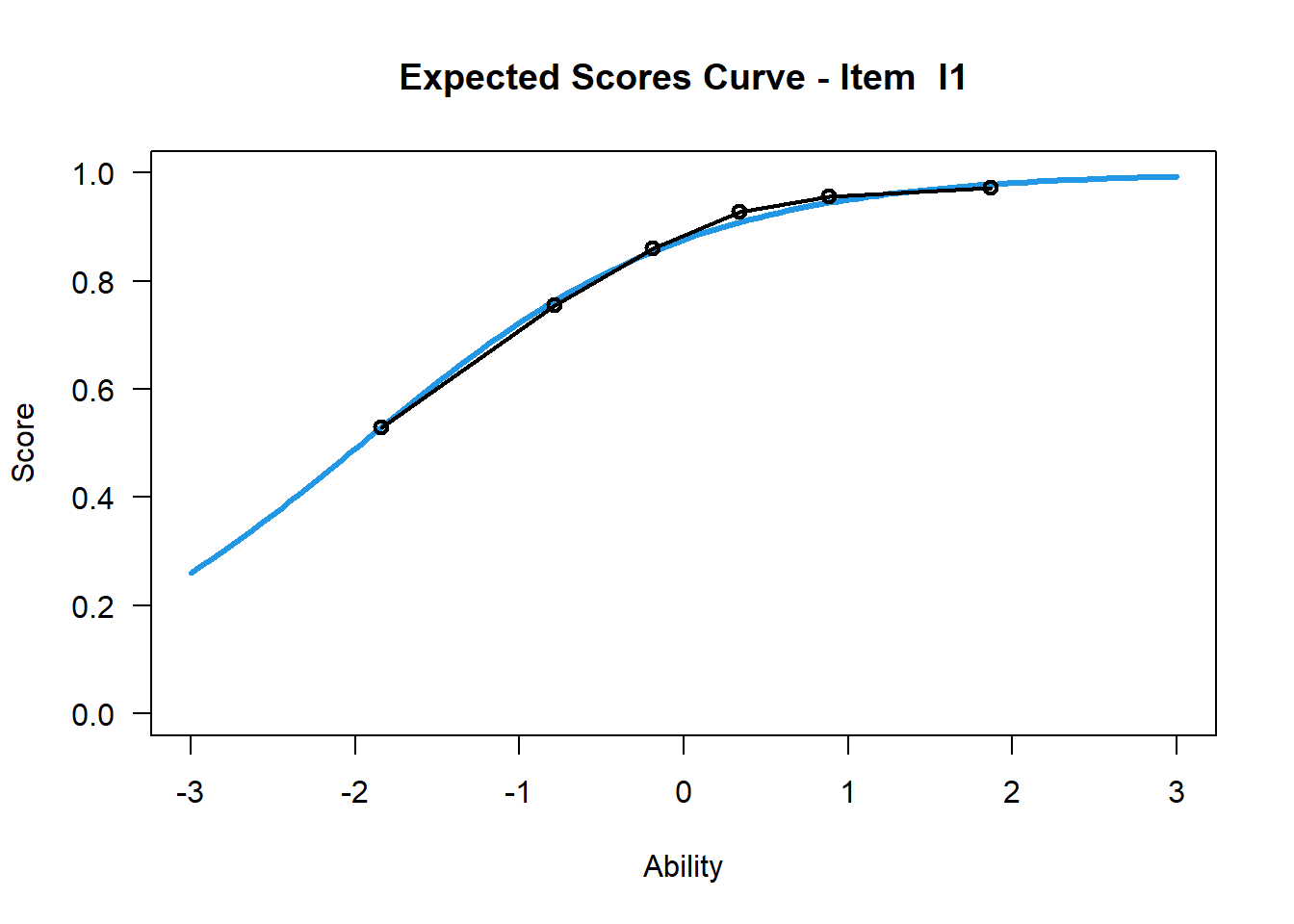
Item 40
plot(mod1, items = 40, ngroups = 6, export = FALSE) # xsi = 2.05## Iteration in WLE/MLE estimation 1 | Maximal change 0.8281
## Iteration in WLE/MLE estimation 2 | Maximal change 0.4335
## Iteration in WLE/MLE estimation 3 | Maximal change 0.0883
## Iteration in WLE/MLE estimation 4 | Maximal change 7e-04
## Iteration in WLE/MLE estimation 5 | Maximal change 0
## ----
## WLE Reliability= 0.894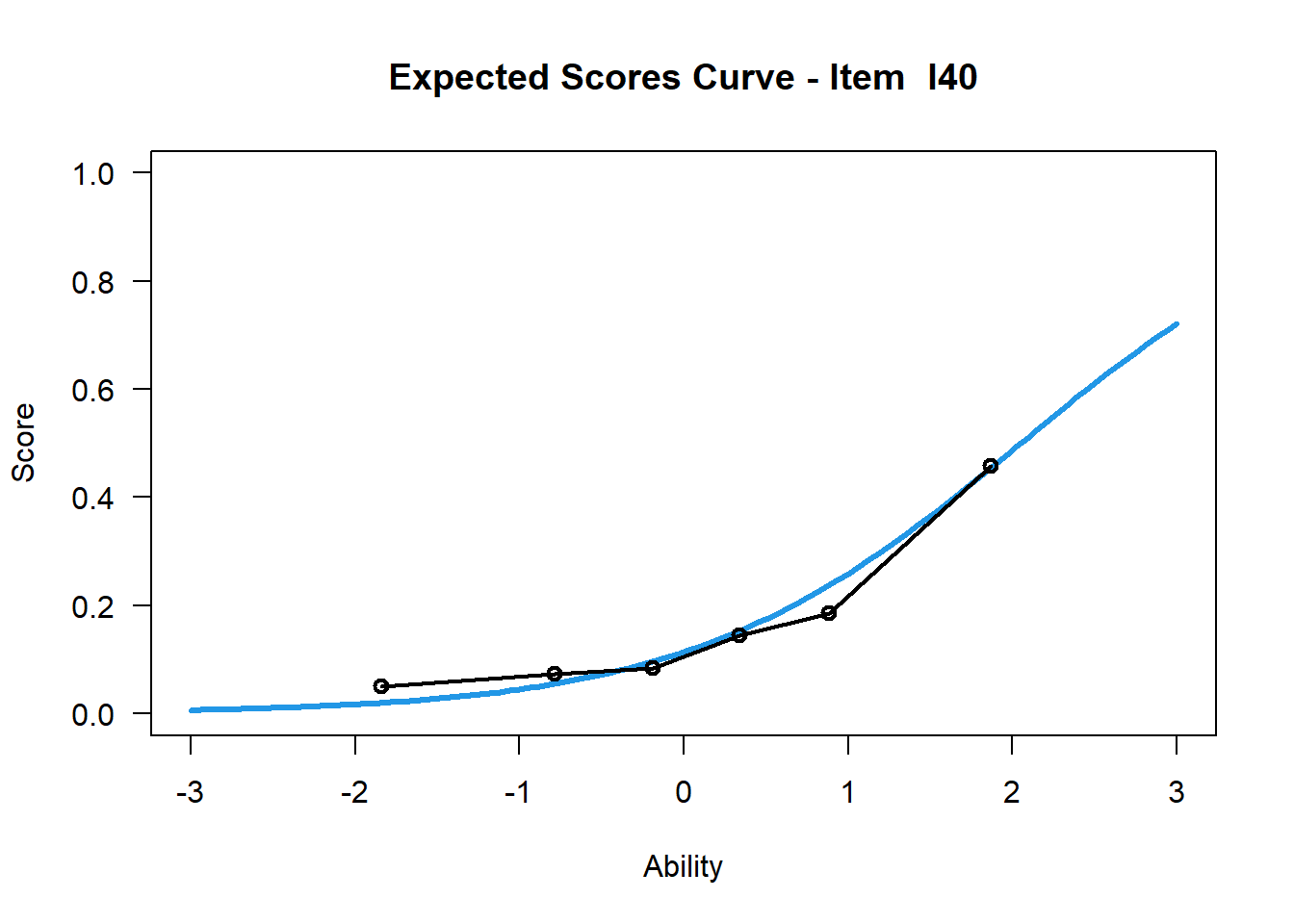
6.6.4.1 Interpretation
Testpersonen mit einer geschätzten Fähigkeit von 0 lösen diese beiden Items mit unterschiedlichen Lösungswahrscheinlichkeiten. Während Testpersonen mit einer Fähigkeitsausprägung von 0 das Item 1 mit etwa 90%iger Wahrscheinlichkeit richtig lösen, lösen diese das Item 40 mit einer etwa 15%igen Lösungswahrscheinlichkeit.
6.6.5 Gegenüberstellung ICC Rasch - 2PL
Item 40 Rasch
plot(mod1, items = 40, ngroups = 6, export = FALSE) # Steigungsparameter = 1## Iteration in WLE/MLE estimation 1 | Maximal change 0.8281
## Iteration in WLE/MLE estimation 2 | Maximal change 0.4335
## Iteration in WLE/MLE estimation 3 | Maximal change 0.0883
## Iteration in WLE/MLE estimation 4 | Maximal change 7e-04
## Iteration in WLE/MLE estimation 5 | Maximal change 0
## ----
## WLE Reliability= 0.894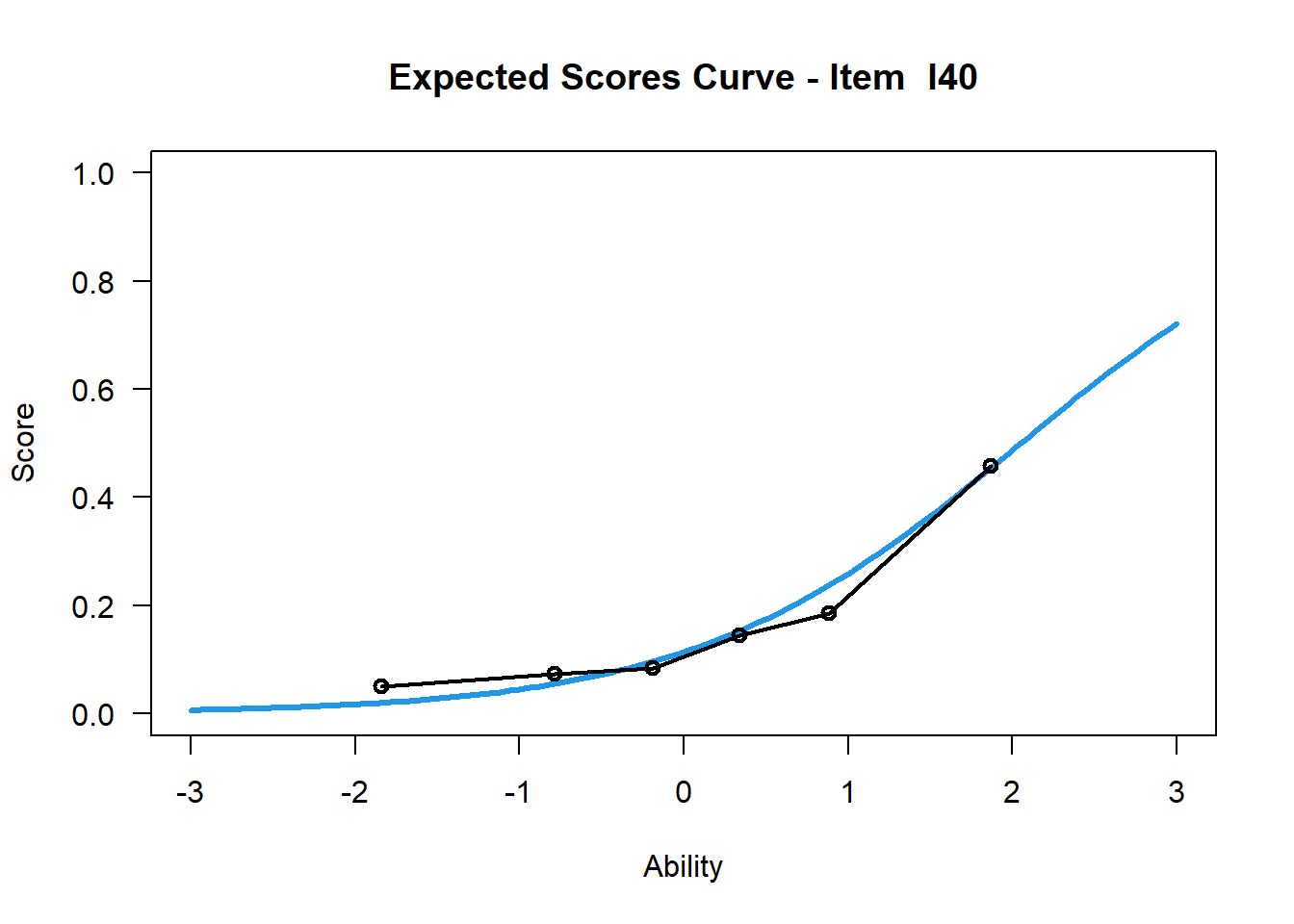
Item 40 2PL
plot(mod2, items = 40, ngroups = 6, export = FALSE) # Steigungsparameter frei geschätzt## Iteration in WLE/MLE estimation 1 | Maximal change 0.3445
## Iteration in WLE/MLE estimation 2 | Maximal change 0.0677
## Iteration in WLE/MLE estimation 3 | Maximal change 5e-04
## Iteration in WLE/MLE estimation 4 | Maximal change 0
## ----
## WLE Reliability= 0.894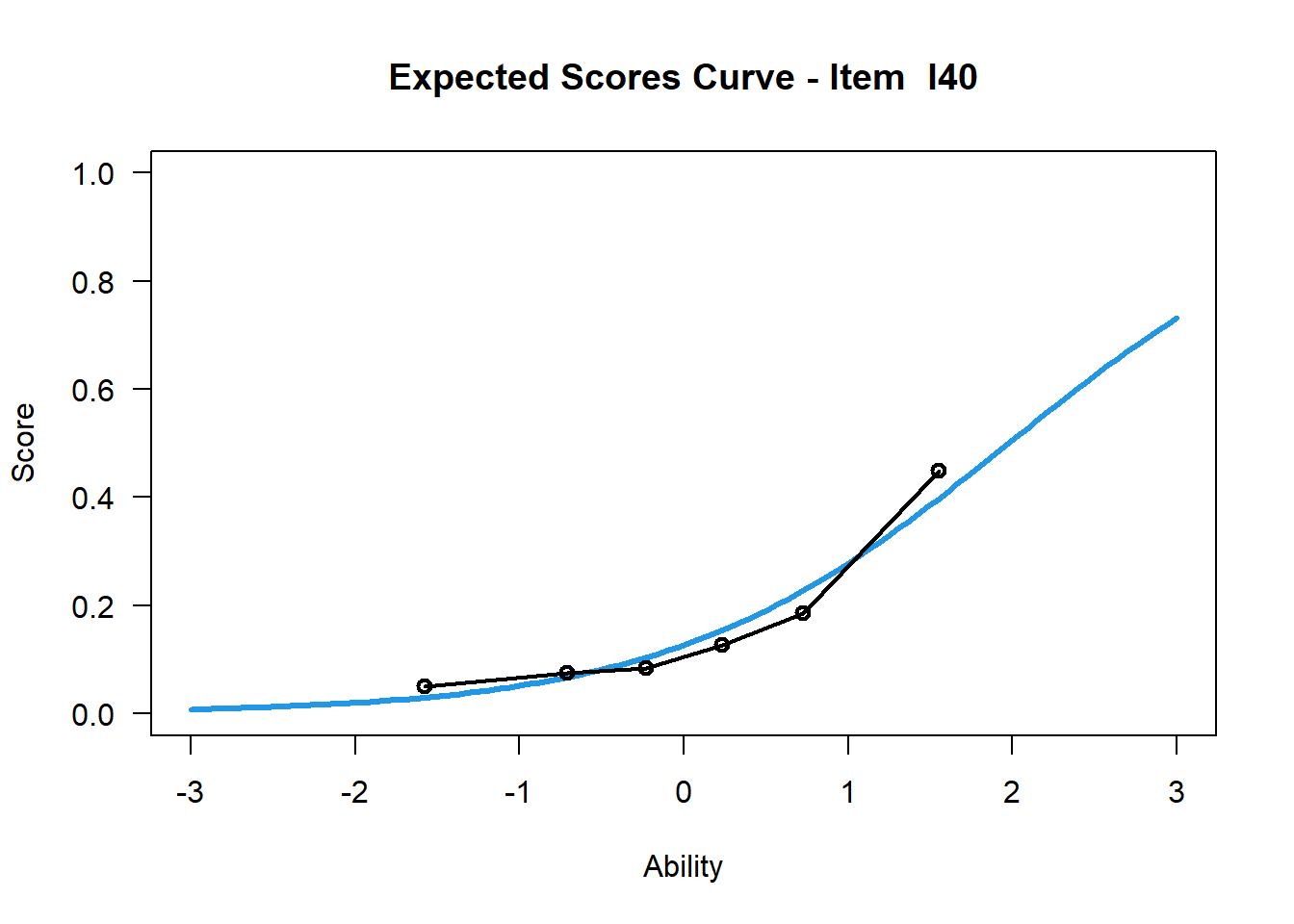
6.6.5.1 Deutung
Beim 2PL Modell wird der Steigungsparameter für jedes Item frei geschätzt. Das zeigt sich unter anderem in den ICCs. Durch das Vorliegen des simulierten Datensatzes zeigt sich kein merkbarer Unterschied in den ICCs des Rasch und 2PL Modells. Dennoch sei an dieser Stelle angemerkt, dass es beim 2PL Modell durchaus zu ICCs kommen kann, die negative Steigungsparameter aufweisen. Die Interpretation dahinter wäre: Bei steigender Personenfähigkeit, sinkt die Lösungswahrscheinlichkeit des Items. Dies kann ein Indiz für ein nicht funktionierendes Item sein, aber ebenso ein Hinweis auf eine Mehrdimensionalität des Konstruktes (Bühner, 2011, S. 506; Chalmers, 2015, S. 216). Jenes Item könnte demnach in eine andere Dimension fallen.